Fractional vortices

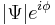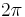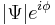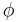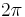In a standard superconductor, described by a complex field $|\Psi|e^{i\phi}$ (condensates wave function), vortices carry quantized magnetic field: a consequence of $2\pi$ -invariance of the phase $\phi$ of the condensate wave function $|\Psi|e^{i\phi}$ . There a winding of the phase ${\phi}$ by $2\pi$ creates a vortex which carries one flux quantum. See Quantum vortex.

The term Fractional vortex is used for two kinds of very different quantum vortices which occur when:

(i) A physical system allows phase windings different from 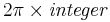$2\pi \times \mathit{integer}$ . I.e. non-integer or fractional phase winding. Quantum mechanics prohibits it in a uniform ordinary superconductor. But it becomes possible in an inhomogeneous system for example if a vortex is placed on a boundary between two superconductors which are connected only by an extremely weak link (also called Josephson Junction), such a situation also occurs in some cases in polycrystalline samples on grain boundaries etc. At such superconducting boundaries the phase can have a discontinous jump. Correspondingly a vortex placed onto such a boundary acquires a fractional phase windings hence the term fractional vortex. Similar situation occurs in Spin-1 Bose condensates where, a vortex with $\pi$ phase winding can exist if it is combined with a domain of overturned spins.

(ii) Different situation occurs in uniform multicomponent superconductors which allow stable vortex solution with integer phase winding 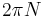$2\pi N$ , where 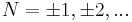$N= \pm 1, \pm 2, ...$ which however carry arbitrarily fractionally quantized magnetic flux.^[1]

1 (i) Vortices with non-integer phase winding
- 1.1 Josephson vortices
  - 1.1.1 Fractional Josephson vortices at phase discontinuities
  - 1.1.2 Vortices on grain boundaries in d-wave superconductors and Josephson Junctions
- 1.2 Spin-triplet Superfluidity
2 (ii) Vortices with integer phase winding and fractional flux in multicomponent superconductivity
3 See also
4 References

(i) Vortices with non-integer phase winding

Josephson vortices

Fractional Josephson vortices at phase discontinuities

Josephson phase discontinuities may appear in specially designed long Josephson junctions (LJJ). For example, so-called 0- $\pi$ LJJ have a $\pi$ discontinuity of the Josephson phase at a point where 0 and $\pi$ parts join. Josephson phase discontinuities can also be introduces using artificial tricks, e.g. 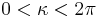a pair of tiny current injectors attached to one of the superconducting electrodes of the LJJ ^[2] .^[3] .^[4] We will denote the value of the phase discontinuity by $\kappa$ and, without losing generality, assume that $0<\kappa<2\pi$ , because the phase is 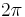$2\pi$ periodic.

LJJ reacts to the phase discontinuity by bending the Josephson phase 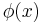$\phi(x)$ in the 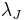$\lambda_J$ vicinity of the discontinuity point, so that far away there are no traces of this perturbation. Bending of the Josephson phase inevitably results in appearance of a local magnetic field 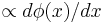$\propto d\phi(x)/dx$ localized around discontinuity (0- $\pi$ boundary). 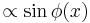It also results in appearance of a supercurrent $\propto\sin\phi(x)$ circulating around discontinuity. 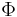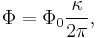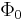The total magnetic flux $\Phi$ , carried by the localized magnetic field, is proportional to the value of the discontinuity $\kappa$ , namely $\Phi = \Phi_0 \frac{\kappa}{2\pi},$ where $\Phi_0$ is a magnetic flux quantum. 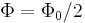For $\pi$ discontinuity, $\Phi=\Phi_0/2$ and the vortex of supercurrent is called a semifluxon. When 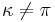$\kappa\neq\pi$ , one speaks about arbitrary fractional Josephson vortices. This type of vortices are pinned at the phase discontinuity point, but may have two polarities, positive and negative, distinguished by the direction of the fractional flux and direction of the supercurrent (clockwise or counterclockwise) circulating around its center (discontinuity point) .^[5]

Semifluxon is a particular case of such a fractional vortex pinned at the phase discontinuity point.

Although, such fractional Josephson vortices are pinned, they, if perturbed, may perform a small oscillations around the phase discontinuity point with the eigenfrequency, which depends on the value of $\kappa$ .^[6] .^[7] .

This type of fractional Josephson vortices may find applications in classical and quantum information storage and processing as well as to build tunable band gap materials for the frequency range of the order of the Josephson plasma frequency.^[8]

Vortices on grain boundaries in d-wave superconductors and Josephson Junctions

In context of d-wave superconductivity, a Fractional vortex known also as splinter vortex is a vortex of supercurrent carrying unquantized magnetic flux, in oppose to conventional Josephson vortex and semifluxons. Fractional vortices exist in the so-called 0-π long Josephson junctions dense chains. Fractional vortices are solitons which are able to move and preserve their shape much like conventional Josephson vortices and in opposed to semifluxons which are attached to the boundary between 0 and π regions.

Theoretically one can obtain an effective double sin-Gordon equation for the phase difference between the two superconducting banks of the 0-π long Josephson junctions dense chains. This is done by taking the asymptotic expansion of the phase difference equation of motion to the second order which results in

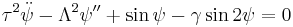
$\tau^2\ddot{\psi}-\Lambda^2\psi''%2B\sin\psi-\gamma\sin2\psi=0$

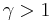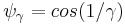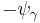where $\gamma$ is a dimensionless constant defined by the junction's properties. The detailed mathematical procedure is similar to the one done for a parametrically driven pendulum, see for example^[9] and ^[10] , and can be extended to time dependent phenomena.^[11] For $\gamma>1$ he above equation for the phase, ψ, has two stable equilibrium values $\psi_{\gamma}=cos(1/\gamma)$ and $-\psi_{\gamma}$ . There are two fractional vortices which correspond to these two values one carries Φ₁= ψ_γΦ₀/π flux and the other carries Φ₂= Φ₀-Φ₁ flux where Φ₀ is the fundamental unit of magnetic flux quantum.

For the first time fractional vortices were observed using d-wave superconductors at asymmetric 45° grain boundaries YBa₂Cu₃O_7-δ . In these systems the phase shift of π takes place inside the d-wave superconductor and not at the barrier. Due to the advent of controlled coupling by proper chosen ferromagnetic thicknesses, 0–π JJs have also recently been realized in low-T_c SFS-like systems ^[12] and underdamped SIFS-type .^[13]

Spin-triplet Superfluidity

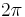In certain states of spin-1 superfluids or Bose condensates condensate's wavefunction is invariant if to change a superfluid phase by $\pi$ , along with a $\pi$ rotation of spin angle. This is in contrast to $2\pi$ invariance of condensate wavefunction in a spin-0 superfluid. A vortex resulting from such phase windings is called fractional or half-quantum vortex, in contrast to one-quantum vortex where a phase changes by 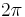$2\pi$ .^[14]

(ii) Vortices with integer phase winding and fractional flux in multicomponent superconductivity

Different kind of "Fractional vortices" appears in the different context in multi-component superconductivity where several independent charged condensates or superconducting components interact with each other electromagnetically. Such a situation occurs for example in the 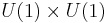$U(1)\times U(1)$ theories of the projected quantum states of liquid metallic hydrogen, where two order parameters originate from theoretically anticipated coexistence of electronic and protonic Cooper pairs. There topological defects with an 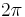$2\pi$ (i.e. "integer") phase winding only in electronic or only in protonic condensate carries fractionally quantized magnetic flux: a consequence of electromagtnetic interaction with the second condensate. Also these fractional vortices carry a superfluid momentum which does not obey Onsager-Feynman quantization ^[15] ^[16] Despite the integer phase winding, the basic properties of this kind of fractional vortices are very different from Abrikosov vortex solutions. For example in contrast to Abrikosov vortex their magnetic field, generically is not exponentially localized in space. Also in some cases the magnetic flux inverts its direction at a certain distance from the vortex center ^[17]

References

Mints, R. G. and Papiashvili, Ilya and Kirtley, J. R. and Hilgenkamp, H. and Hammerl, G. and Mannhart, J. (2002). "Observation of Splintered Josephson Vortices at Grain Boundaries in YBa₂Cu₃O_7-δ". Phys. Rev. Lett. 89 (6): 067004. Bibcode 2002PhRvL..89f7004M. doi:10.1103/PhysRevLett.89.067004.

Mints, R. G. (1998). "Self-generated flux in Josephson junctions with alternating critical current density". Phys. Rev. B 57 (6): R3221. doi:10.1103/PhysRevB.57.R3221.

C. C. Tsuei and J. R. Kirtley (2002). "d-Wave pairing symmetry in cuprate superconductors --- fundamental implications and potential applications". Physica C 367 (1-4): 1. doi:10.1016/S0921-4534(01)00976-5.

and

^ [1]. Egor Babaev, Phys.Rev.Lett. 89 (2002) 067001.
^ A. Ustinov (2002). "Fluxon insertion into annular Josephson junctions". Appl. Phys. Lett. 80 (17): 3153–3155. doi:10.1063/1.1474617.
^ B. A. Malomed and A. V. Ustinov (2004). "Creation of classical and quantum fluxons by a current dipole n a long Josephson junction". Phys. Rev. B 69 (6): 064502. doi:10.1103/PhysRevB.69.064502.
^ E. Goldobin, A. Sterck, T. Gaber, D. Koelle, R. Kleiner (2004). "Dynamics of semifluxons in Nb long Josephson 0- 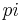$pi$ junctions". Phys. Rev. Lett. 92 (5): 057005. Bibcode 2004PhRvL..92e7005G. doi:10.1103/PhysRevLett.92.057005. PMID 14995336.
^ E. Goldobin, D. Koelle, R. Kleiner (2004). "Ground states of one and two fractional vortices in long Josephson 0- $\kappa$ junctions". Phys. Rev. B 70 (17): 174519. doi:10.1103/PhysRevB.70.174519.
^ E. Goldobin, H. Susanto, D. Koelle, R. Kleiner, S. A. van Gils (2005). "Oscillatory eigenmodes and stability of one and two arbitrary fractional vortices in long Josephson 0- $\kappa$ junctions". Phys. Rev. B 71 (10): 104518. doi:10.1103/PhysRevB.71.104518.
^ K. Buckenmaier, T. Gaber, M. Siegel, D. Koelle, R. Kleiner, E. Goldobin (2007). "Spectroscopy of the Fractional Vortex Eigenfrequency in a Long Josephson 0- $\kappa$ Junction". Phys. Rev. Lett. 98 (11): 117006. Bibcode 2007PhRvL..98k7006B. doi:10.1103/PhysRevLett.98.117006. PMID 17501081.
^ H. Susanto, E. Goldobin, D. Koelle, R. Kleiner, S. A. van Gils (2005). "Controllable plasma energy bands in a one-dimensional crystal of fractional Josephson vortices". Phys. Rev. B 71 (17): 174510. doi:10.1103/PhysRevB.71.174510.
^ L. D. Landau and E. M. Lifshitz (1994). Mechnics, Pergamon press, Oxford.
^ V. I. Arnold, V. V Kozlov, and A. I. Neishtandt (1997). Mathematical aspects of classical and celestial mechnics, Springer.
^ M. Moshe and R. G. Mints (2007). "Shapiro steps in Josephson junctions with alternating critical current density". Phys. Rev. B 76 (5): 054518. doi:10.1103/PhysRevB.76.054518.
^ M. L. Della Rocca, M. Aprili, T. Kontos, A. Gomez and P. Spathis (2005). "Ferromagnetic 0-π Junctions as Classical Spins". Phys. Rev. Lett 94 (19): 197003. Bibcode 2005PhRvL..94s7003D. doi:10.1103/PhysRevLett.94.197003. PMID 16090200.
^ M. Weides, M. Kemmler, H. Kohlstedt, R. Waser, D. Koelle, R. Kleiner and E. Goldobin (2006). "0-π Josephson Tunnel Junctions with Ferromagnetic Barrier". Phys. Rev. Lett 97 (24): 247001. Bibcode 2006PhRvL..97x7001W. doi:10.1103/PhysRevLett.97.247001. PMID 17280309.
^ Dieter Vollhardt , Peter Woelfle The Superfluid Phases Of Helium 3 (1990)
^ [2]. Egor Babaev, "Vortices with fractional flux in two-gap superconductors and in extended Faddeev model" Phys.Rev.Lett. 89 (2002) 067001.
^ [3]. Egor Babaev, N. W. Ashcroft "Violation of the London Law and Onsager-Feynman quantization in multicomponent superconductors" Nature Physics 3, 530 - 533 (2007).
^ [4]. Egor Babaev, Juha Jaykka, Martin Speight, " Magnetic field delocalization and flux inversion in fractional vortices in two-component superconductors" Phys. Rev. Lett 103, 237002 (2009).